In discussing what a “perfect” display would be, the common view could be said like this:
But recently, I have been coming to the conclusion that we should describe the problem in this way:
Said another way:
This leads to the real question:
That is the heart of it. Does every single cone inside our eye do something that affects our vision? If so, a perfect display needs to be about 4x of visual acuity in each dimension.
How steep is that edge? Here is a more concrete example. Let us say that we have three cones in a row detecting if there is a dip in the signal. I.e. they are resolving a feature.
In this case, cone A records HIGH, cone B records LOW, and cone C records HIGH. From this information, the eye does not know how wide that frequency is, only that it is less than the size of the distance between A and C, or twice the spacing of the cones.
If you think about it, there are two operations that happen in resolving a frequency. First, the drop in levels (from A to B) and then the rise (from B to C). But each of those features is interesting by themselves.
Here are three more cases.
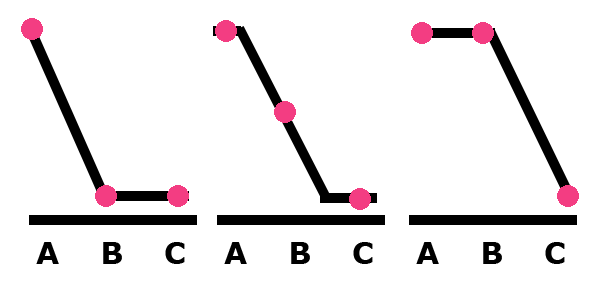
In these three cases, the signal is the same but shifted over half of our spacing. All three cases have the same value for A and C, but B shifts. Is it plausible that the change in value from that single cone is enough to change our perception of the scene. My opinion: YES!
Note that the middle case is somewhat ambiguous. There are three different ways that the signal could be which cause the the HIGH-MED-LOW sampling of the signal.
If we have only this information, we do not know if the slope of the drop is the first, second, or third case. All that we know is that the falloff is thinner than twice our cone spacing. The length of the drop could be 2x our cone spacing, 1x our cone spacing, or it could be 0.01x our cone spacing.
But, if we have a 2d grid of sample points, we can use nearby rows to make an educated guess.

The middle row by itself does not have enough information to determine the width of the dropoff. It only knows that the dropoff is 2x cone spacing. But the top and bottom rows both have enough information to determine that the width must be less than 1x cone spacing, and our eye can use that information to guess the information in the middle row. Logically, our eye should be able to figure out that the width of the gradient is less than one cone spacing width.

This case has a wider line that is a little over the spacing of one cone. Our cones should be able to figure out that this gradient has wider spacing because two cones from each row are in the gradient, whereas in the sharper example zero or one cone from each row are in the gradient.
Keep in mind that our reconstruction could be incorrect.

In this situation, the middle row is actually quite blurry and that gradient is wider than one cone spacing. Since this situation is unlikely to happen in the real world, our eye will likely guess it to be a consistent, hard edge. It is impossible to accurately reconstruct this signal with our given cone spacing. But whether our eye reconstructs the scene correctly or incorrectly is irrelevant. A perfect display would need to create a signal that causes our eye to make the same reconstruction mistakes that it would see in the real world.
Note 1: Vernier acuity takes this phenomenon a step further. By looking at the slope of the line across many rows, our eye can make an estimate of where the center of that line is and detect misalignment.
Note 2: Sometimes our eye guesses wrong. When you see a very thin, sharp line, our eye estimates that as a wider, softer line. If we want to simulate reality, we need a high enough display to accurately stimulate our cones to make those same incorrect guesses.
Note 3: The world is not point sampled. Our cones have a physical size and the projected image is slightly out of focus so a perfectly sharp line will always be slightly blurred. As long as our eyes know how much expected blur there is, they should be able to determine that falloff of the original line is less than the cone spacing.
Note 4: Does this actually happen? Not sure. But it seems plausible, and I have yet to see proof either way.
Edge Sharpness Acuity Here is another interesting question: What is “Edge Sharpness Acuity”? It is not actually a scientific term–I just made it up. But what is the resolution where we can tell the difference between a sharp edge and a blurry edge? Has anyone actually studied this? It seems like the kind of thing that someone probably has studied but my google skills failed me. Keep in mind, the usual definition of “sharpness” is resolvable resolution, whereas I am talking about the slope of an edge.
Theoretically it should be possible to determine if a an edge is within 1x the spacing of our cones. If we can detect two edges within 2x the spacing of our cones to resolve a signal, then it seems plausible that we can detect a single edge within 1x or our cone spacing, especially given the nearby information of other cones.
Anecdotally, this seems like it might be true. When I look at a 4k display, it seems obviously better than a 2k display. But it could be that the 4k display had better content. Even though I can not resolve smaller points, it is possible that I can tell that the edges are “sharper”. Then again, maybe I am just the victim of confirmation bias because I want to believe that 4k displays matter. Maybe I was fooled when the sales guy at Best Buy told me that 4k displays have “30% more color”. He actually said that.
But if “Edge Sharpness Acuity” exceeds Visual Acuity, then we definitely can not fake this effect with supersampling on a lower res display. While edge aliasing can be detected at 5x to 10x the resolution of visual acuity, it seems like we could just render with high MSAA and solve the problem even with a display that is only at the resolution of visual acuity. But if the sharpness of the edge can be detected at higher than the resolution of visual acuity, the only way to fool our eye is with a higher res display.
Conclusions This discussion gets me back to the original question:
Those charts you have seen about the importance of resolution vs viewing distance usually assume that each cone DOES NOT matter, and that we only need displays to exceed visual acuity. But if every cone does matter and every cone does affect how our eye guesses at what the scene should be, then we need to go higher.
We can arrive at visual acuity by saying that the cones in our eye need twice the resolution of our screen. But is that backwards? If we reverse this problem and want to recreate the sampling for every single cone, then our display needs twice the resolution of the cone spacing in our eye.
So that is where 4x comes from. We need to double visual acuity to get back to cone spacing, and we need to double it again because our display (the sampler) needs twice the resolution of the ground truth surface (the cone spacing in our retina). To have a perfect display that is indistinguishable from real life, my conjecture is that the upper bound on screen resolution is 4x visual acuity in each dimension.
Said another way, here is that image again with three values for A, B, and C.

We need to have a display that is high enough resolution to create a signal that preserves A and C but allows us to twiddle the value of B. Based on Nyquist-Shannon, that signal would need to have twice the resolution of our cone spacing.
Finally, I need to make a few caveats:
- I am making a very weak statement. I am not saying that we definitely need a display that has 4x visual acuity in each dimension. Just that we might need that much resolution, and we need to fully study hyperacuity before we can definitively say what the upper limit on resolution of a screen needs to be. In this post I am not trying to prove anything. Rather, I am explaining my conjecture that 4x visual acuity would be enough. But it is just that, a conjecture. Saying that the eye could theoretically act a certain way based on cone placement does not mean that it actually does.
- 4x visual acuity might not actually be compelling. It is plausible that there are effects which we can see all the way up to that resolution, but those effects are unimportant and not worth the cost.
- Even with a display at 4x visual acuity, we would still need anti-aliasing. Vernier acuity is from 5x to 10x visual acuity, so even on a display with such tightly packed pixels we would need anti-aliasing.
- This discussion ignores temporal resolution. Our eyes are much more sensitive to crawling jaggies than static jaggies. Eyes are constantly moving (microsaccades). The two phenomena might be related. It is not impossible that our eye can somehow use temporal information, but I have not seen strong evidence either. I find it hard to believe that temporal information from microsaccades can determine information about a scene that exceeds 4x visual acuity. My guess would be that the eye does not know exactly how far it has moved each "frame" and reconstructs the estimated position from the visual information. But I do not know of any studies that prove or disprove this possibility.
Finally, it seems like this phenomena should have been studied by somebody. The perception of screen resolution should be important to many large electronics companies. So if you have seen any information that either proves or disproves this conjecture then please share!
comments powered by Disqus
