What resolution does a display need to have before you can not perceive aliasing? The discussion usually goes something like this:
- The human eye has a visual acuity of about 1 arc minute.
- If a display has a resolution that exceeds 1 arc minute, it exceeds visual acuity.
- Therefore, such a display exceeds the resolution of the human eye. We don’t need to worry about aliasing, and there is no use in having a higher resolution display because they eye can not perceive it.
This argument has a major logical flow: Statement #3 is incorrect. “Visual Acuity” is completely different from “What the eye can see”, also known as Hyperacuity. If you want a display that is so good that it exceeds everything that the eye can do, then you need to exceed Hyperacuity, not Visual Acuity.
Visual Acuity First up, what is visual acuity? It’s the same concept as resolvable resolution. The image from the scene goes through the lens of the eye and gets projected on the retina.

The above image comes from the wikipedia page on Color Blindness. The left shows the distribution of foveal cones in normal vision and the right shows the distribution of a color blind person. But the important thing to note is the spacing of the cones.
By definition 20/20 vision means that the viewer can detect a gap in a line as long as that gap is at least 1 arc minute. Note: An arc minute is 1/60th of a degree. In other words, Visual Acuity is the same as resolvable resolution. Scientists have measured the physical spacing of the rods and cones in the eye (more importantly, the cones of the fovea) and people with visual acuity of 1 arc minute tend to have their cones spaced about half that distance apart.
Visual Acuity in practice is closely related to the Nyquist limit. With your cones spaced 0.5 arc minutes apart, you need three cones to determine that there is a gap. Two of the cones need to be “on”, and you need one to be “off” in between them. The smallest detail that can be resolved is the distance between the centers of those two “on” cones. A cone spacing of 0.5 arc minutes gives you visual acuity of 1.0 arc minutes, just as the Nyquist limit says.

Here is an example that I have used before. If you look closely at the crosses you should be able to see that some of the crosses are solid and others are made of small dots. Stand as far away from your computer screen as you can but still see the difference. Try to figure out the threshold where the dots in the crosses are not resolvable to your eye. At this distance, if this screen had 2x the resolution it would not matter because the screen resolution is already beyond the resolvable limit.
Edge Aliasing Now look at this image. You should clearly be able to see the edges that have aliasing versus the ones that are smooth. Go back as far as you can from your screen until you can not see any difference. Try it.
If you are a human, you should be able to see the stair-stepping in the edges at a much greater distance than you could resolve the dots in the crosses. So what is going on here? Both features are one pixel wide. But for some reason that edge aliasing feature is much stronger. It’s a phenomena known as Vernier Acuity, and it is a form of Hyperacuity. In fact, we can detect slightly misaligned thin lines with 5x to 10x more precision than Visual Acuity.
What about signal theory? How is this effect possible? Signal theory is very well studied, and it tells us that we should not be able to resolve features that are smaller than 1 arc minute (assuming we have 20/20 vision with cone spacing of 0.5 arc minutes). Yet, somehow we can detect aliasing well below that threshold.
Is signal theory wrong? Did Nyquist and Shannon make a mistake in the sampling theorem? Of course not. The problem is that the Nyquist-Shannon theorem has one major caveat: NO PRIOR KNOWLEDGE! The sampling theorem is based on the assumption that you are trying to reconstruct frequencies from samples and nothing else. But if you have prior knowledge about the structure of the scene, then you can determine information about your scene that exceeds the resolvable resolution of your samples.
Example #1: Subpixel Corner Detection A trivial example is subpixel corner detection. If you have ever used OpenCV, you have probably calibrated a checkerboard like this.
In most cases you should be able to detect the location of the checkerboard corners with subpixel precision. Of course, without prior knowledge this would be impossible. But with prior knowledge (we know that it is a checkerboard with straight lines) we can accumulate the data and discover subpixel information about our scene.
Example #2: Edge Aliasing The Wikipedia article on Vernier Acuity has this nice image which in a way explains the crosses vs lines image above. The top two features demonstrate resolvable resolution. In order to determine that the two features are separated, we need to have a complete mosaic element (a cone) in between them to resolve that difference.
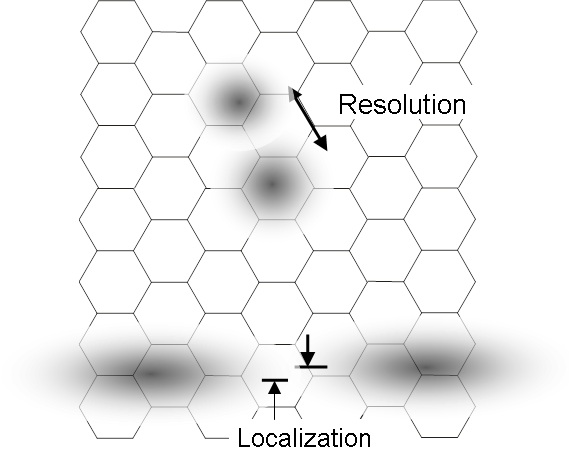
However, for the two features at the bottom, we can tell that they are misaligned. Note that due to imperfect focus, each foveal cone will return the approximate intensity of the blurred feature on that cone. From the relative intensities, the eye can determine where the center of the line passes through the mosaic pattern and figure out the misalignment with high accuracy. This phenomena is called Vernier Acuity.
Example #3: VR and Stereoscopic Acuity If you work in VR then you should also be aware of Stereoscopic Acuity, which is another form of Hyperacuity. In the tests cited by this wikipedia article, the typical detectable interocular separation of two eyes is 0.5 arc minutes, or about half of visual acuity (1 arc minute). At a range of 6 meters, the detectable depth would be 8cm. If we want users to be able to perceive virtual worlds with the same depth precision as the real world, that likely means that we need to hit double resolution of visual acuity. Getting the resolution of a VR display to match Visual Acuity is going to be hard enough, but we potentially need to quadruple that (2x in 2 dimensions) to achieve a perception of depth that matches reality.
Although it depends on the type of stimulus. In the Other Measures section, for complex objects stereo acuity is similar to visual acuity. But for vertical rods it can apparently be as low as 2 arc seconds (1/30th of an arc minute). In other words, 30x as strong as typical visual acuity. Call me crazy, but I don’t think we’ll be seeing VR displays with a resolution of 2 arc seconds any time soon.
Conclusion #1: “What the eye can see” greatly exceeds Visual Acuity Hopefully it is clear that the eye can see features that exceed the limits of resolvable resolution. To completely fool the human eye, having enough resolution to exceed Visual Acuity is not sufficient. Rather, we need to have enough resolution to fool the heuristics and pattern matching capabilities of our complete visual system. To hit that threshold we need to exceed Hyperacuity, not Visual Acuity.
Conclusion #2: We still need AA in games? Um, yes. It is not even close. If we want to have displays that are so good that we don’t need to worry about aliasing, then we need between 5x to 10x higher resolution than Visual Acuity.
Conclusion #3: What resolution is “enough”? One counterargument is that we do not actually need to create high resolution displays to exceed the limits of hyperacuity. For example, if we were to create an image with perfect super-sampling then we should be able to downscale it and fix all of our aliasing issues. Would that resolution be good enough to fool our abilities to detect aliasing? For VR, would exact (and expensive) supersampling allow us to achieve full stereoscopic acuity? Would that strategy allow us to exceed all of forms of Hyperacuity in our visual system? Would the image still seem sharp? I’ll talk about it a little more in my next post. The answer: Definitely maybe.
But if we want to claim that a display with resolution X is enough to exceed “what they eye can see”, we need to prove it. We need to understand all the different forms of hyperacuity and have a reasonable explanation for how all those forms of hyperacuity can be recreated with such a display. We also need to verify these findings with clinical studies if we really, really want to be sure. But it is not acceptable to say resolution X exceeds Visual Acuity, sprinkle some pixie dust on it, and claim that it exceeds “what the eye can see”.
comments powered by Disqus
