Why Reinhard Desaturates Your Blacks

One thing I’ve mentioned is that if you use the simplest Reinhard tonemapping operator, then you will get desaturated blacks. In this image, the top row is using Reinhard, the middle is straight linear, and the bottom is using Filmic Tonemapping by HP Duiker. Also, there are many different forms of Reinhard, so the one I’m using is x/(x+1) for each color channel.

If you look at them, Reinhard has more desaturated blacks than either a linear or a filmic curve. Why is this?

Suppose that we have a color that is an RGB triple of (.50,.25,.25). This will be reddish, and the green and blue are both 50% of red. Now let’s apply Reinhard to this.

Red: .50/(1+.50) = .33 Green: .25/(1+.25) = .20 Blue: .25/(1+.25) = .20

You may have noticed that the numbers as a whole went down, but don’t worry about that. If you are using any tonemapping operator, you are playing so much with the luminance anyway that you should be compensating for whatever the tonemapping operator is doing. The real issue is that now green and blue are now 60% of red. So by doing this operation, you have desaturated your color. Why does the curve do this?

Here is a comparison between a linear curve and Reinhard.

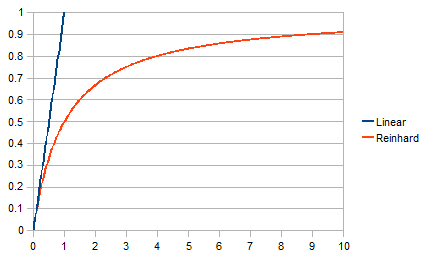
Reinhard works by bringing down the high values. If the maximum output on your display is 1.0, then a linear curve hits that max at, well, 1.0. Whereas linear goes to infinity and beyond, Reinhard asymptotically goes to 1.0, but never hits it. Try plugging a million into x/(x+1).

But this causes problems if you use it on your 3 RGB values separately. The higher your value, the more it brings it down. That’s why Reinhard desaturates your blacks: It brings up the lower channels. Of course you can solve this problem by converting your colors to from RGB to HSL, doing Reinhard on luminance, and converting from HSL back to RGB.

In general, we can say that any tonemapping operation that is concave-downwards (i.e. has a positive first derivative and a negative second derivative) at the low end will desaturate your blacks. That’s what gives the Reinhard curve the feeling of a “gray film” in front of the camera.